Summer projects are scheduled for the UIC 8-week session (June 13 – Aug 5) unless otherwise specified. The application deadline for full consideration is May 6, 2016. Accepted students may be able to arrange lab orientation and access before the official project start date.
Project: Circle packing visualization
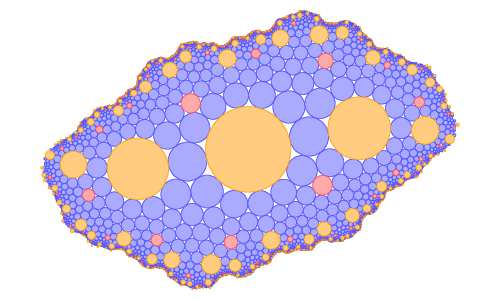
Faculty supervisor: David Dumas
Graduate mentor: Ellie Dannenberg
Student researchers: Kimberly Kim and Jacob Lewis
Project type: Summer undergraduate team research
Dates: 13 June to 5 August 2016 (UIC 8-week session)
Description: Circle packings are arrangements of circles in the plane, the sphere, or on a more general surface that have tangencies in a prescribed pattern. This project will focus on developing software tools for constructing, deforming, and visualizing finite circle packings on compact surfaces of higher genus, and of associated symmetric infinite circle packings in the plane with (an example of which is shown above).
Prerequisites: This project requires familiarity with the Python computer programming language. The only required mathematical background is multivariable calculus and linear algebra. Knowledge of abstract algebra (particularly group theory), topology (e.g. the fundamental group), or complex analysis would be useful but is not required.
Materials
Project: Immersive visualization of data sets in the 3-sphere
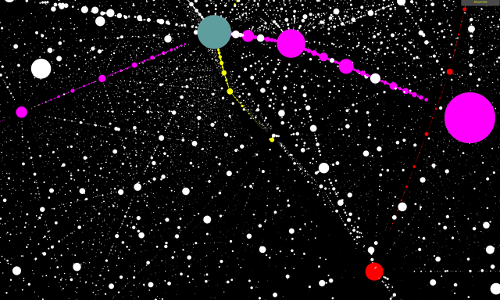
Faculty supervisor: David Dumas
Student researchers: Galen Ballew and Alexander Gilbert
Project type: Summer undergraduate team research
Dates: 13 June to 5 August 2016 (UIC 8-week session)
Description: In this continuation of a Fall 2015 project, students will continue development of real-time 3D graphics programs for visualization of point-cloud data sets in the 3-dimensional sphere, targeting both virtual reality platforms (such as Oculus Rift) and desktop computers. The primary focus will be on datasets related to the geometry and combinatorics of curves on compact hyperbolic surfaces.
Prerequisites: This project requires multivariable calculus, linear algebra, and experience with the Unity 3D graphics engine.
Materials
Project: Random graphs

Faculty supervisor: Benjamin Antieau
Graduate mentor: Sam Cole
Project type: Summer high school team research
Dates: 20 June to 15 July 2016
Description: A graph is a mathematical structure consisting of nodes (“vertices”) and connections between the nodes (“edges”). Graphs can be used to model anything from molecules to social networks to the internet. For example, the vertices of a graph could represent users on Facebook, and two people are connected by an edge if they are friends. We can then ask questions like “how many ‘steps’ does it take to get from one person to another through mutual friends?” Sometimes, graphs are formed randomly. Then we can ask: what properties are very likely for a random graph to have, and what properties are very unlikely? We will investigate some of these properties and use software to explore them numerically.
