Spring 2018 Projects

Project: 3D Printing Surfaces

Project supervisor: Daniel Groves
Graduate mentor: Paul Rapoport
Student researchers: Mario Aranda, Xuchen Wang, Dean Welby, Amal Yaghmour

Description: This project will explore surfaces in three-dimensional space by 3D printing models of them. The goal is to start by choosing appropriate equations and end with physical models which would be appropriate for use in multivariable calculus classes. This will involve learning about function graphing software, 3D modeling software and 3D printing. Time and student interest permitting, we can investigate such things as curvature, ruled surfaces and other things which touch upon ideas from topology, geometry and algebraic geometry.

Outcomes: The outcome of our research project produced interesting and appealing results of 3D models from common equations from multivariable calculus and later, a “twist” on them. At first, we chose simple equations to get adjusted of 3D model software from Wolfram Mathematica and exporting such models to be edited in Blender. Later, we exported the files to the STL or OBJ format, allowing them to be opened in the slicing software Cura that is used with the Ultimaker 2 3D printer. Early attempts of such did not always produce adequate results since the procedure at times had to be adjusted because of either file exporting, software, or printer issues that occurred. However, as time went on we became more familiar with 3D modeling software, solved the issue with exporting and importing files, and avoided further printer issues. In conclusion, our research project consisted of using functions related to multivariable calculus, learning how to model and print 3D models with modeling software, and exploring some less common shapes and functions to generate interesting models.

Materials and resources:

Project: Efficiency of Planar Disk Packings

Project Supervisor: Ali Mohajer
Student researchers: Rohit Banerjee, Ivan Cruz, Jacob Krol

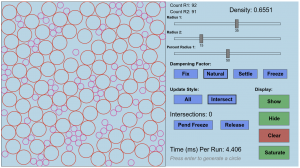
Description: A popular chemistry experiment shows that a mixture of certain pure liquids can be denser than each of the constituents. Mixing a liter of methanol with a liter of ethanol gives a solution with volume measurably less than 2 liters! A mathematical analog of this experiment is the fact that a packing of unequal disks in the plane can be denser than a packing of equal disks, as long as the radii of the disks aren’t very close. Exactly how close is “very close” is an area of active research. In fact, much remains to be discovered about the behavior of two-species packings, except at a handful of very special ratios of radii where everything fits together very nicely. In this research project we will study randomly generated two-species packings in order to gain insight into the shape of the density bounding function.

Outcomes: We initially attempted to develop an understanding of the bounding density curves of disk packings by creating an interactive visualization where the user could add various sized disks and manipulate them under a simulation of almost gaseous physics. We then turned to determining a thorough method for evaluating the saturation of a given palette of disks. Though we were able to make great strides in a rigorous testing method, using additively-weighted Voronoi decompositions, our project concluded without substantial data using this method. Instead, our final data was drawn with an experimental method of adding and deleting disks until a satisfyingly saturated palette was achieved. In addition to the relatively large size of the disks and possible inaccuracies in our data collection, our methods should be sharpened in the future to evaluate the validity of our final results.

Materials and resources: