Project: Visualizing Fractals Using 3D Printing

Project supervisor: Olga Lukina
Student researchers: Divye Bhagwani, Harsha Podapati, Theodore Spiro
Description: Fractals are self-similar patterns that are created by repeating a geometric construction over and over at smaller and smaller scales. Patterns with fractal characteristics occur naturally in nature, for example, a snowflake or a leaf of a plant may have a structure resembling fractals. In mathematics, we can construct a variety of fractals using iterated function systems, or using substitutions. During this project we will use 3D printing to visualize simple fractals in three dimensions.
Outcomes: Throughout the semester, we researched and learned about various types of fractals, as well as the different techniques that are employed to create them. We also learned about the mathematical properties of the fractals we printed. For instance, some fractals have the property of having a dimension less than three when they are generated.
After researching a particular fractal, we set out to create a program to generate it, and then proceeded to create a physical 3D model. To create our 3D prints, we programmed our designs into the software OpenSCAD, which created 3D renderings of the objects. Then, we would export the rendered models to Cura, the 3D printing software. Once in the 3D printing software, we could adjust the size and settings for each print. We then experimented with different printing settings until the prints were of the desired quality.
Materials and resources:
- Poster
- Collection of 3D printing meshes (zip download)
Project: Destructive Topology: Slicing Surfaces in VR

Project supervisor: David Dumas
Student researchers: Alexander Adrahtas, Alexander Guo, Gregory Schamberger
Description: Closed surfaces (like the torus shown above) can be constructed by stitching together the sides of a polygon according to a certain pattern. However, it can be difficult to visualize what a pattern drawn inside the polygon would look like when wrapped around the surface, or conversely, what a design on the surface would look like when unwrapped to the flat polygon.
The purpose of this project is to develop a virtual reality mathematical visualization and teaching tool that will allow users to explore this correspondence (between flat polygons and curved surfaces). Building on a prototype developed in Unity 3D by Professor Dumas, the student researchers in this project will create a virtual surface laboratory where the user can slice, stitch, paint, and manipulate surfaces in space while seeing the same operations performed on the corresponding flat polygons.
Outcomes: The main outcome of our research project was successfully re-creating and improving upon the mathematical visualization tool GenusView into the virtual reality mathematical visualization tool GenusLab. Aside from the added perspective into the relationship between the geometry of surfaces and the hyperbolic plane allowed by virtual reality, GenusLab incorporated a number of improvements that allow users to more deeply explore this relationship. Some of the improvements include the ability to grab the genus-two surface, the option to drill through the genus-two surface, an intuitive UI, changing the color used to draw on the surfaces, and changing the background texture of the genus-two surface and the hyperbolic plane. In creating this tool, we gained a deeper understanding of hyperbolic geometry, working in the game engine Unity, creating software for virtual reality, writing shader programs, coding in C#, and we learned the nuances of collaborative software development.
Materials and resources:
- Poster
- VR application GenusLab VR 0.5:
- Source code repository
Project: Two-radius Planar Disk Packings

Project supervisor: Ali Mohajer
Student researchers: Jacob Krol, Rohit Banerjee
Description: The densest packing of disks of the same radius in the plane is the hexagonal lattice. If disks of two different radii are allowed, it is sometimes possible to pack disks more densely than the hexagonal lattice, however this is only possible if the ratio of the radii is not very close to one. Exactly how close is “very close” is an area of active research, and much remains to be discovered about the behavior of two-radius packings. In this research project we will study the densities of randomly generated two-radius disk packings with various ratios of radii, with a goal of obtaining experimental insights into the variation of the optimal density as the ratio of radii changes.
This project will build on the results of the Spring 2018 MCL semester project Efficiency of Planar Disk Packings.
Outcomes: As a continuation of our previous work on this subject, we were able to utilize systems that we had already developed while implementing more mathematically-rigorous methods to further our research. Using our gaseous physics engine, we placed it in the context of a larger data collector which used the physics algorithms in tandem with Voronoi; decompositions to automate the process of creating and saturating a palette with disks of given radii and proportion. Additively-weighted Voronoi decompositions allowed us to decompose the plane into cells, drawn with their edges and vertices defined by being equidistant from the nearest neighboring disks. Testing this finite list of vertices, therefore, could exhaustively check the possibility of adding a new disk at any point in our finite plane. With this implementation, we could consistently draw densities for various initial conditions for two-species packings. Obtaining curves that were slightly different from expected in shape and y-intercept suggests a need for further investigation into these patterns. A necessary next step for this research would involve decreasing the complexity of our physics algorithms to improve run-time and, in turn, allow for larger samples that better approximate an infinite space.
Materials and resources:
Project: Robot Kinematics
Project supervisor: Julius Ross
Student researchers:Ativ Aggarwal, Leticia Garcia, Sara Sayeed
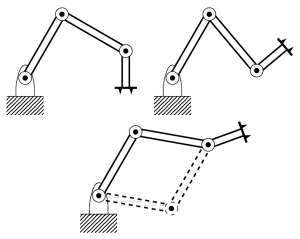
Description: Robot kinematics considers the following kinds of problems. Imagine a robot arm made up of a number of straight segments joined together by hinges. One end of the arm is fixed on a table and at the other end is a tip (or finger) of some kind. Suppose the robot wants to move its finger to a give point, then what angles must it choose for each of the joints? Is it the case that the robot can move its finger to any position, or are there some that it cannot reach? What about if it wants to move its finger to a given position and make it point in a given direction? One can ask this question in either two dimensions or three dimensions (or even more!).
This project will consider these questions by understanding the problem as finding solutions to a system of simultaneous polynomial equations, which then becomes a problem in numerical algebraic geometry.
Outcomes: This project allowed us to develop a much stronger understanding of the topic of robot kinematics. Initially, we learned about robot kinematics from the book Ideals, Varieties, and Algorithms by Cox, Little, and O’Shea. This allowed us to grasp a basic understanding and foundation of our project. We went through various exercises and lessons together as a group to solidify our understanding.
After understanding this topic better we moved onto solving problems in two dimensions. Specifically, we worked on computing the positions of each part of a robot when given the dimensions and relative positions of its components. This portion took us a long time, but was critical to our work. After this theoretical portion we then experimented with an actual robotic arm to start applying all of our accumulated knowledge. In doing so we developed codes in order to make the robot move in different ways. From here we learned that many constraints and restrictions are present in the physical robot. If there was more time this would have been one of the things we would have liked to delve deeper into. Overall, this project allowed us to gain a good sense of problem solving, cooperation, and time management.
Materials and resources:
